Understanding the View Matrix

Posted on by

In this article, I will attempt to explain how to construct the view matrix correctly and how to use the view matrix to transform a model’s vertices into clip-space.  I will also try to explain how to compute the camera’s position in world space (also called the Eye position) from the view matrix.

Introduction

Understanding how the view matrix works in 3D space is one of the most underestimated concepts of 3D game programming.  The reason for this is the abstract nature of this elusive matrix.  The world transformation matrix is the matrix that determines the position and orientation of an object in 3D space. The view matrix is used to transform a model’s vertices from world-space to view-space.  Don’t be mistaken and think that these two things are the same thing!

You can think of it like this:

Imagine you are holding a video camera, taking a picture of a car. You can get a different view of the car by moving your camera around it and it appears that the scene is moving when you view the image through your camera’s view finder.  In a computer program the camera doesn’t move at all and in actuality, the world is just moving in the opposite direction and orientation of how you would want the camera to move in reality.

In order to understand this correctly, we must think in terms of two different things:

  1. The Camera Transformation Matrix: The transformation that places the camera in the correct position and orientation in world space (this is the transformation that you would apply to a 3D model of the camera if you wanted to represent it in the scene).
  2. The View Matrix: This matrix will transform vertices from world-space to view-space.  This matrix is the inverse of the camera’s transformation matrix.
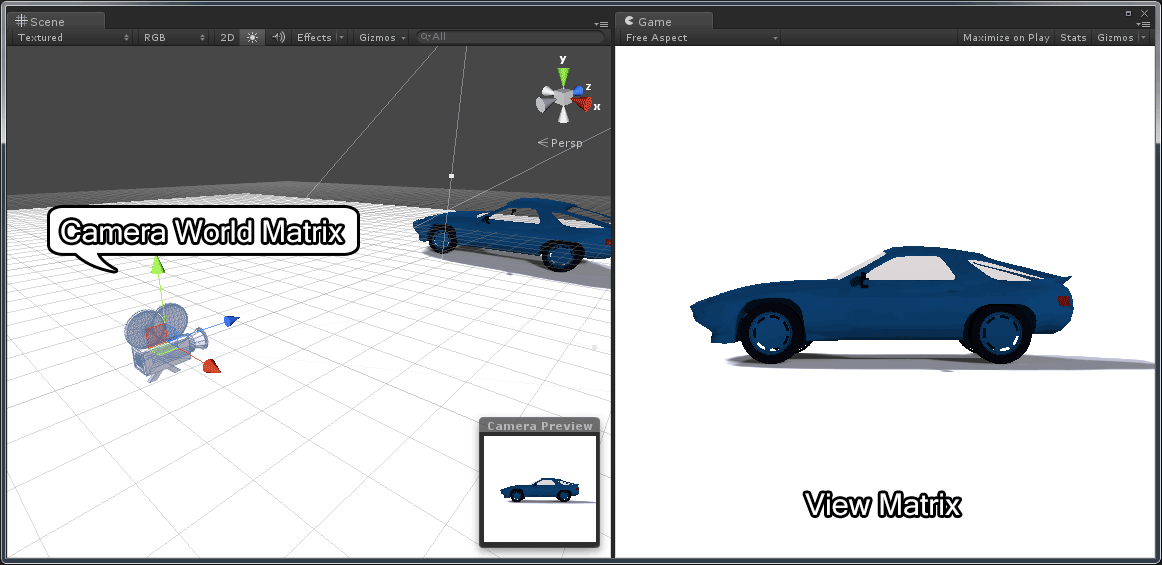
Camera World Matrix vs View Matrix

Camera World Matrix vs View Matrix – The model of the car is from Nate Robin’s OpenGL tutorials (http://user.xmission.com/~nate/tutors.html).

In the image above, the camera’s world transform is shown in the left pane and the view from the camera is shown on the right.

Convention

In this article I will consider matrices to be column major. That is, in a 4×4 homogeneous transformation matrix, the first column represents the “right” vector (\(\mathbf{X}\)), the second column represents the “up” vector (\(\mathbf{Y}\)), the third column represents the “forward” vector (\(\mathbf{Z}\)) and the fourth column represents the translation vector (origin or position) (\(\mathbf{W}\)) of the space represented by the transformation matrix.

\[\begin{bmatrix}right_x & up_x & forward_x & position_x \\ right_y & up_y & forward_y & position_y \\ right_z & up_z & forward_z & position_z \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

Using this convention, we must pre-multiply column vectors to transform a vector by a transformation matrix. That is, in order to transform a vector \(\mathbf{v}\) by a transformation matrix \(\mathbf{M}\) we would need to pre-multiply the column vector \(\mathbf{v}\) by the matrix \(\mathbf{M}\) on the left.

\[\begin{matrix}
\mathbf{v}’ & = & \mathbf{M}\mathbf{v} \\
\begin{bmatrix} x’ \\ y’ \\ z’ \\ w’\end{bmatrix} & = & \begin{bmatrix} m_{0,0} & m_{0,1} & m_{0,2} & m_{0,3} \\ m_{1,0} & m_{1,1} & m_{1,2} & m_{1,3} \\ m_{2,0} & m_{2,1} & m_{2,2} & m_{2,3} \\ m_{3,0} & m_{3,1} & m_{3,2} & m_{3,3} \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix}
\end{matrix}\]

The elements of the matrix \(\mathbf{M}\) are written \(m_{i,j}\) which represents the element in the \(i^{th}\) row and the \(j^{th}\) column of the matrix.

And to concatenate a set of affine transformations (such translation (\(\mathbf{T}\)), scale (\(\mathbf{S}\)), and rotation (\(\mathbf{R}\))) we must apply the transformations from right to left:

\[\mathbf{v}’=(\mathbf{T}(\mathbf{R}(\mathbf{S}\mathbf{v})))\]

This transformation can be stated in words as “first scale, then rotate, then translate”. The \(\mathbf{S}\), \(\mathbf{R}\), and \(\mathbf{T}\) matrices can also be concatenated to represent a single transformation:

\[\begin{array}{rcl}
\mathbf{M} & = & \mathbf{T}\mathbf{R}\mathbf{S} \\
\mathbf{v}’ & = & \mathbf{M}\mathbf{v}
\end{array}\]

And to transform a child node in a scene graph by the transform of it’s parent you would pre-multiply the child’s local (relative to it’s parent) transformation matrix by it’s parents world transform on the left:

\[\mathbf{Child}_{world}=\mathbf{Parent}_{world} * \mathbf{Child}_{local}\]

Of course, if the node in the scene graph does not have a parent (the root node of the scene graph) then the node’s world transform is the same as its local (relative to its parent which in this case is just the identity matrix) transform:

\[\mathbf{Child}_{world}=\mathbf{Child}_{local}\]

Memory Layout of Column-Major Matrices

Using column matrices, the memory layout of the components in computer memory of a matrix are sequential in the columns of the matrix:

\[\mathbf{M} = \begin{bmatrix} m_{0,0} & m_{1,0} & m_{2,0} & \cdots & m_{3,3} \end{bmatrix}\]

This has the annoying consequence that if we want to initialize the values of a matrix we must actually transpose the values in order to load the matrix correctly.

For example, the following layout is the correct way to load a column-major matrix in a C program:

At first glance, you will be thinking “wait a minute, that matrix is expressed in row-major format!”. Yes, this is actually true. A row-major matrix stores it’s elements in the same order in memory except the individual vectors are considered rows instead of columns.

So what is the big difference then? The difference is seen in the functions which perform matrix multiplication. Let’s see an example.

Suppose we have the following C++ definitions:

The vec4 structure provides an index operator to allow for the use of indices to access the individual components of the vector. This will make the code slightly easier to read. It is interesting to note that the vec4 structure could be interpreted as either a row-vector or a column-vector. There is no way to differentiate the difference within this context.

The mat4 structure provides an index operator to allow for the use of indices to access the individual columns (not rows!) of the matrix.

Using this technique, in order to access the \(i^{th}\) row and the \(j^{th}\) column of matrix \(\mathbf{M}\), we need to access the elements of the matrix like this:

This is quite annoying that we have to swap the \(i\) and \(j\) indices in order to access the correct matrix element. This is probably a good reason to use row-major matrices instead of column-major matrices when programming however the most common convention in linear algebra textbooks and academic research papers is to use column-major matrices. So the preference to use column-major matrices is mostly for historical reasons.

Suppose now that we define the following functions:

The first function performs pre-multiplication of a 4-component column vector with a 4×4 matrix. The second method performs post-multiplication of a 4-component row vector with a 4×4 matrix.
And the third method performs 4×4 matrix-matrix multiplication.

Then the pre-multiply function would look like this:

Notice that we still multiply the rows of matrix m with the column vector v but the indices of m simply appear swapped.

And similarly the function which takes a 4-component row-vector v and pre-multiplies it by a 4×4 matrix m.

In this case we multiply the row vector v by the columns of matrix m. Notice that we still need to swap the indices to access the correct column and row of matrix m.

And the final function which performs a matrix-matrix multiply:

This function multiplies the rows of m1 by the columns of m2. Notice we have to swap the indices in both m1 and m2.

This function can be written slightly simplified if we reuse the pre-multiply function:

The main point is that whatever convention you use, you stick with it and be consistent and always make sure you document clearly in your API which convention you are using.

Transformations

When rendering a scene in 3D space, there are usually 3 transformations that are applied to the 3D geometry in the scene:

  1. World Transform: The world transform (or sometimes referred to as the object transform or model matrix) will transform a models vertices (and normals) from object space (this is the space that the model was created in using a 3D content creation tool like 3D Studio Max or Maya) into world space. World space is the position, orientation (and sometimes scale) that positions the model in the correct place in the world.
  2. View Transform: The world space vertex positions (and normals) need to be transformed into a space that is relative to the view of the camera. This is called “view space” (sometimes referred to “camera space”) and is the transformation that will be studied in this article.
  3. Projection Transform: Vertices that have been transformed into view space need to be transformed by the projection transformation matrix into a space called “clip space”. This is the final space that the graphics programmer needs to worry about. The projection transformation matrix will not be discussed in this article.

If we think of the camera as an object in the scene (like any other object that is placed in the scene) then we can say that even the camera has a transformation matrix that can be used to orient and position it in the world space of the scene (the world transform, or in the context of this article, I will refer to this transform as the “camera transform” to differentiate it from the “view transform”). But since we want to render the scene from the view of the camera, we need to find a transformation matrix that will transform the camera into “view space”. In other words, we need a transformation matrix that will place the camera object at the origin of the world pointing down the Z-axis (the positive or negative Z-axis depends on whether we are working in a left-handed or right-handed coordinate system. For an explanation on left-handed and right-handed coordinate systems, you can refer to my article titled Coordinate Systems). In other words, we need to find a matrix \(\mathbf{V}\) such that:

\[\mathbf{I}=\mathbf{V}\mathbf{M}\]

Where \(\mathbf{M}\) is the camera transform matrix (or world transform), and \(\mathbf{V}\) is the view matrix we are looking for that will transform the camera transform matrix into the identity matrix \(\mathbf{I}\).

Well, it may be obvious that the matrix \(\mathbf{V}\) is just the inverse of \(\mathbf{M}\). That is,

\[\mathbf{V}=\mathbf{M}^{-1}\]

Coincidently, The \(\mathbf{V}\) matrix is used to transform any object in the scene from world space into view space (or camera space).

The Camera Transformation

The camera transformation is the transformation matrix that can be used to position and orient an object or a model in the scene that represents the camera.  If you wanted to represent several cameras in the scene and you wanted to visualize where each camera was placed in the world, then this transformation would be used to transform the vertices of the model that represents the camera from object-space into world space. This is the same as a world-matrix or model-matrix that positions any model in the scene.  This transformation should not be mistaken as the view matrix.  It cannot be used directly to transform vertices from world-space into view-space.

To compute the camera’s transformation matrix is no different from computing the transformation matrix of any object placed in the scene.

If \(\mathbf{R}\) represents the orientation of the camera, and \(\mathbf{T}\) represents the translation of the camera in world space, then the camera’s transform matrix \(\mathbf{M}\) can be computed by multiplying the two matrices together.

\[\mathbf{M}=\mathbf{T}\mathbf{R}\]

Remember that since we are dealing with column-major matrices, this is read from right-to-left. That is, first rotate, then translate.

The View Matrix

The view matrix on the other hand is used to transform vertices from world-space to view-space.  This matrix is usually concatenated together with the object’s world matrix and the projection matrix so that vertices can be transformed from object-space directly to clip-space in the vertex program.

If \(\mathbf{M}\) represents the object’s world matrix (or model matrix), and \(\mathbf{V}\) represents the view matrix, and \(\mathbf{P}\) is the projection matrix, then the concatenated world (or model), view, projection can be represented by \(\mathbf{MVP}\) simply by multiplying the three matrices together:

\[\mathbf{MVP}=\mathbf{P}*\mathbf{V}*\mathbf{M}\]

And a vertex \(\mathbf{v}\) can be transformed to clip-space by multiplying by the combined matrix \(\mathbf{MVP}\):

\[\mathbf{v}’=\mathbf{MVP}*\mathbf{v}\]

So that’s how it’s used, so how is the view matrix computed? There are several methods to compute the view matrix and the preferred method usually depends on how you intend to use it.

A common method to derive the view matrix is to compute a Look-at matrix given the position of the camera in world space (usually referred to as the “eye” position), an “up” vector (which is usually \(\begin{bmatrix} 0 & 1 & 0 \end{bmatrix}^T\)), and a target point to look at in world space.

If you are creating a first-person-shooter (FPS), you will probably not use the Look-at method to compute the view matrix. In this case, it would be much more convenient to use a method that computes the view matrix based on a position in world space and pitch (rotation about the \(\mathbf{X}\) axis) and yaw (rotation about the \(\mathbf{Y}\) axis) angles (usually we don’t want the camera to roll (rotation about the \(\mathbf{Z}\) axis) in a FPS shooter).

If you want to create a camera that can be used to pivot around a 3D object, then you would probably want to create an arcball camera.

I will discuss these 3 typical camera models in the following sections.

Look At Camera

Using this method, we can directly compute the view matrix from the world position of the camera (eye), a global up vector, and a target point (the point we want to look at).

A typical implementation of this function (assuming a right-handed coordinate system which has a camera looking in the\(\mathbf{-Z}\) axis) may look something like this:

This method can be slightly optimized because we can eliminate the need for the final matrix multiply if we directly compute the translation part of the matrix as shown in the code below.

In this case, we can take advantage of the fact that taking the dot product of the x, y, and z axes with the eye position in the 4th column is equivalent to multiplying the orientation and translation matrices directly. The result of the dot product must be negated to account for the “inverse” of the translation part.

A good example of using the gluLookAt function in OpenGL can be found on Nate Robins OpenGL tutor page: http://user.xmission.com/~nate/tutors.html

FPS Camera

If we want to implement an FPS camera, we probably want to compute our view matrix from a set of euler angles (pitch and yaw) and a known world position. The basic theory of this camera model is that we want to build a camera matrix that first rotates pitch angle about the \(\mathbf{X}\) axis, then rotates yaw angle about the \(\mathbf{Y}\) axis, then translates to some position in the world. Since we want the view matrix, we need to compute the inverse of the resulting matrix.

\[\mathbf{V}=(\mathbf{T}(\mathbf{R}_y\mathbf{R}_x))^{-1}\]

The function to implement this camera model might look like this:

In this function we first compute the axes of the view matrix. This is derived from the concatenation of a rotation about the \(\mathbf{X}\) axis followed by a rotation about the \(\mathbf{Y}\) axis. Then we build the view matrix the same as before by taking advantage of the fact that the final column of the matrix is just the dot product of the basis vectors with the eye position of the camera.

Arcball Orbit Camera

An arcball (orbit) camera is commonly used to allow the camera to orbit around an object that is placed in the scene. The object doesn’t necessarily need to be placed at the origin of the world. An arcball camera usually doesn’t limit the rotation around the object like the FPS camera in the previous example. In this case, we need to be aware of the notorious Gimbal-lock problem. If you are not familiar with the Gimbal-lock problem, then I suggest you read about it here or watch this video created by GuerrillaCG:

The Gimbal-lock problem can be avoided by using quaternions but Gimbal-lock is not the only problem when using Euler angles to express the rotation of the camera. If the camera is rotated more than 90° in either direction around the \(\mathbf{X}\) axes, then the camera is upside-down and the left and right rotation about the \(\mathbf{Y}\) axes become reversed. In my experience, this is a really hard problem to fix and most applications simply don’t allow the camera to rotate more than 90° around the \(\mathbf{X}\) axes in order to avoid this problem altogether. I found that using quaternions is the only reliable way to solve this problem.

Refer to my previous article titled Understanding Quaternions for a tutorial on how to work with quaternions.

If you are using a mouse, you may want to be able to rotate the camera around an object by clicking and dragging on the screen. In order to determine the rotation, the point where the mouse was clicked on the screen (\(\mathbf{p}_0\)) is projected onto a unit sphere that covers the screen. When the mouse is moved, the point where the mouse moves to (\(\mathbf{p}_1\)) is projected onto the unit sphere and a quaternion is constructed that represents a rotation from \(\mathbf{p}_0\) to \(\mathbf{p}_1\). Working with quaternions is beyond the scope of this article. For a complete explanation on how to compute a quaternion from two points, refer to this article: http://lolengine.net/blog/2013/09/18/beautiful-maths-quaternion-from-vectors. The GLM math library also provides a quaternion class that has a constructor that takes two vectors and computes the rotation quaternion between those two vectors.

To construct the view matrix for the arcball camera, we will use two translations and a rotation. The first translation (\(\mathbf{t}_0\)) moves the camera a certain distance away from the object so the object can fit in the view. Then a rotation quaternion (\(\mathbf{r}\)) is applied to rotate the camera around the object. If the object is not placed at the origin of the world, then we need to apply an additional translation (\(\mathbf{t}_1\)) to move the pivot point of the camera to the center of the object being observed. The resulting matrix needs to be inverted to achieve the view matrix.

\[\begin{array}{rcl}
\mathbf{M} & = & \mathbf{T}_1\mathbf{R}\mathbf{T}_0 \\
\mathbf{V} & = & \mathbf{M}^{-1}
\end{array}\]

If you know that the object will always be at the origin, then \(\mathbf{T}_1\) represents the identity matrix (\(\mathbf{I}\)) and can be omitted from the equation.

The function to implement an arcball orbit camera might look like this:

You can avoid the matrix inverse on line 12 if you pre-compute the inverse of the individual transformations and swap the order of multiplication.

I have not fully tested the source code shown in the Arcball function so use at your own risk!

Converting between Camera Transformation Matrix and View Matrix

If you only have the camera transformation matrix \(\mathbf{M}\) and you want to compute the view matrix \(\mathbf{V}\) that will correctly transform vertices from world-space to view-space, you only need to take the inverse of the camera transform.

\[\mathbf{V}=\mathbf{M}^{-1}\]

If you only have the view matrix \(\mathbf{V}\) and you need to find a camera transformation matrix \(\mathbf{M}\) that can be used to position a visual representation of the camera in the scene, you can simply take the inverse of the view matrix.

\[\mathbf{M}=\mathbf{V}^{-1}\]

This method is typically used in shaders when you only have access to the view matrix and you want to find out what the position of the camera is in world space. In this case, you can take the 4th column of the inverted view matrix to determine the position of the camera in world space:

\[\begin{array}{rcl}
\mathbf{M} & = & \mathbf{V}^{-1} \\
\mathbf{eye}_{world} & = & \begin{bmatrix} \mathbf{M}_{0,3} & \mathbf{M}_{1,3} & \mathbf{M}_{2,3} \end{bmatrix}
\end{array}\]

Of course it may be advisable to simply pass the eye position of the camera as a variable to your shader instead of inverting the view matrix for every invocation of your vertex shader or fragment shader.

Download the Demo

This OpenGL demo shows an example of how to create an first-person and a look-at view matrix using the techniques shown in this article. I am using the OpenGL Math Library (https://github.com/g-truc/glm) which uses column-major matrices. The demo also shows how to transform primitives correctly using the formula:

\[\mathbf{M}=\mathbf{T}\mathbf{R}\mathbf{S}\]

Where

  • \(\mathbf{T}\) is a translation matrix.
  • \(\mathbf{R}\) is a rotation matrix.
  • \(\mathbf{S}\) is a (non-uniform) scale matrix.

See line 434 in main.cpp for the construction of the model-view-projection matrix that is used to transform the geometry.

ViewMatrixDemo.zip

Usage:

Run the ViewMatrixDemo.exe in the bin folder.

  • Space: Toggle scale animation.
  • Shift: Speed up camera movement.
  • W: Move camera forward.
  • A: Move camera left.
  • S: Move camera backward.
  • Q: Move camera upwards.
  • E: Move camera downwards.
  • LMB: Rotate the camera.
  • RMB: Rotate the geometry.
  • R: Reset the camera to it’s default position and orientation.
  • Esc: Quit the demo.
View Matrix Demo

View Matrix Demo

Conclusion

I hope that I have made clear the differences between the camera’s transform matrix and the view matrix and how you can convert between one and the other. It is also very important to be aware of which matrix you are dealing with so that you can correctly obtain the eye position of the camera. When working with the camera’s world transformation, the eye position is the 4th row of the world transform, but if you are working with the view matrix, you must first inverse the matrix before you can extract the eye position in world space.

69 thoughts on “Understanding the View Matrix”

  1. In other words: the view matrix is the absolute rotation and position of the camera, with the camera’s position inverted, i.e. (8, 8, 8) becomes (-8, -8, -8).

    Reply ↓

  2. Why does the LookAt function return ( translation * orientation ) instead of ( orientation * translation ) ? I think that the second expression is correct.

    Reply ↓

    • Keep in mind that this function is returning the inverse of the camera matrix that would position and orient this camera in world space. That is, the function returns the View matrix.

      And since we know the orientation is orthonormalized then we also know that the inverse is equivalet to the transpose (see Matrices for a evidence that the inverse is equivalent to the transpose in the case of orthonormalized matrices).

      If R is the rotation matrix and T is the translation matrix then we can also write T * R == transpose(R) * T because the only thing we are doing when we change the order of matrix multiplication is making row-major matrices column-major and visa-versa (if we remember from our linear algebra courses).

      Also keep in mind if you are switching from row-major (primarily used in DirectX) to column-major (primarily used in OpenGL) matrices, then you must also change the order in which matrices are multiplied.

      The rule-of-thumb is: If it doesn’t look right, swap your matrix multiplies.

      Reply ↓

      • Ok, so in the LookAt function translation and orientation matrices are in a row-major order, and I should pass GL_TRUE in glUniformMatrix4fv when uploading the LookAt result (translation * orientation)

        Reply ↓

        • You should only transpose a matrix if you are sure you are passing a row-matrix when a column matrix is expected or visa-versa.

          If you are primarily working with column matrices and OpenGL, then I would strongly suggest you use the OpenGL Mathmatics library (http://glm.g-truc.net/). This library has an extensive math library including functions to build view matrices and world transformation matrices (as well as many other features)

          Reply ↓

      • This clears up why the view matrix was returned instead of the inverse view (camera transformation matrix) but one question why does the camera not move and why does the world move ?

        Reply ↓

        • Michael,

          This is a matter of perspective. From the perspective of the camera, the world moves while the camera is stationary. In the view space, the camera is at the origin and everything else in the world is expressed relative to that. Does this make sense?

          Reply ↓

  3. I believe example in the code you provided is in row vector format and the math you have shown could cause confusion. For the Row vector format you would instead multiply v * Model * View * Projection = Clipspace.

    Reply ↓

  4. Thanks for the tutorial. I do have one question though. If the view matrix is just the inverse of the world matrix, what’s the point of making a world-view-projection matrix? Matrix multiplication is associative, so you could write MVP as (MV)P. If V is the inverse of M that would make (MV) the identity matrix I, so (MV)P would be equal to IP, which would be equal to P. And yet I always see MVP used, not just P.

    Reply ↓

    • Xavier,

      That is ONLY true when you are talking about the camera.

      Every object in your scene has it’s OWN world matrix. So a character in your world will have a different world matrix than the camera’s world matrix (referred to as the camera matrix in this article).

      But yes, if you take the camera matrix and multiply it by the view matrix, you will absolutely get the identity matrix. That makes sense if you consider the camera to be fixed at the origin and you simply move the world around you (which is what I said in the first paragraph).

      Reply ↓

  5. I’m trying out a particle system example that came out with RenderMonkey and it uses a “view inverse matrix” to billboard the quads for the particle effect.

    I can see all the values, but I can’t work out how they calculate the “view inverse matrix”, it’s not the inverse of the view matrix or the inverse of the view projection.

    Are you familure with the term, if so how is this calculated?

    Reply ↓

    • The “view inverse matrix” is probably a 3×3 matrix (or a 4×4 matrix with no translation) that represents a matrix that will anti-rotate the particle to face the camera. This matrix cannot take the translation of the camera into consideration because if it did, all of your particles would be placed on the position of the camera.

      In short: it is a matrix that will anit-rotate the particle to always face the camera.

      Reply ↓

    • Thanks Michael for the kind words. I do realize that this article needs to be rewritten to be more clear and maybe include a few examples of working camera models (such as FPS camera, 3rd person camera, or orbit camera). This is on my TODO list.

      Reply ↓

      • sorry, guys but i want someone to correct my ideas if they are wrong
        first, I’m trying to develop a 3d engine but the understanding of with respect to which
        (the camera or the object ) vectors are computed for example when trying to compute the lookAt vector ..should i write camerapos – objectpos or
        objectpos – camerapos ??
        and how to compute the up and right vectors corresponding to the previous determination

        and when to use row-major matrices vs column-major matrices
        and when to right-multiply matrices vs left-multiply matrices

        and how to implement a camera free look rather than looking at a particular object
        and should i use a left handed coordinate system or right handed

        Reply ↓

  7. I’m confused. Given an orientation, R, and a translation, T of a camera, wouldn’t the camera’s transform matrix, M, be T * R? That is, you rotate it, then you translate it? Or do I have that backwards?

    I’m getting frustrated trying to learn this stuff because there’s so many gaps in every resource on the web. For example, in your Matrices tutorial, you describe various matrices, and their properties, but nowhere do you describe the effects of multiplying them together. And finding those effects elsewhere on the web has been really hard.

    I think I need to get a book, sorry this turned into a rant 🙁

    Also, seeing your matrices confused the crap out of me because I didn’t know they were in column major order until I read the comments.

    Reply ↓

    • Brian,

      I’m sorry for the confusion. I do plan on improving this article to include various camera models and explaining the difference between the Right-Handed coordinate systems and Left-Handed coordinate systems and the differences between column matrices and row matrices and the effect it has on the math (the order of the matrix multiples must be reversed if you are using a different system).

      I don’t mind the rant because then I know where I need to improve… It’s just a matter of finding the time to do it!

      Regards,

      Jeremiah

      Reply ↓

  8. I’m confused, based on what I learned in college about linear translations, the last column would be used for translations not the last row. Why isn’t this the case? Aren’t matrices multiplied with vectors row by row?

    Reply ↓

    • In linear algebra, you should have learned this:


      M = A * B ; Mij = sum( Aik * Bkj )

      In words, the elements of the rows of matrix A are multiplied by the elements of the columns of matrix B and their results are summed.
      Also, if you change the order of multiplication, it may change the result (so A * B != B * A). That is, (unlike scalar multiplication) matrix multiplication is not commutative.

      In computer graphics, the 4th row (for row-major matrices) or the 4th column (for column-major matrices) is used to store the translation of the local coordinate system. If you see an example using row-major matrices (as shown here) but you are using column-major matrices, then you only have to change the order of multiplication to get the same results.

      For example:
      If you want to transform a 4-component vector v by a 4×4 matrix M then you must perform the transformation in a specific order dependent on the matrix layout.

      For Row-Major matrices, you must perform the transformation in this order:


      v' = ( v * M );

      For Column-Major matrices, you must perform the transformation in this order:


      v' = ( M * v );

      I hope this makes sense.

      Reply ↓

      • As far as I understood it, exactly the same rules applies to matrix multiplication. So, if you want to apply translation after the rotation in Row-Major you will need to do:

        RT = T * R;

        In Column-Major:

        RT = R * T;

        In a way, Column-Major multiplication order is really confusing, I think.

        Reply ↓

  9. For OpenGL: First of all regarding the notation I am going to use: As it is the convention in OpenGL (see OpenGL Specification and the OpenGL Reference Manual) I use Column-Major notation for matrices. Moreover, as this is the case in OpenGL, the application of transformations is seen from right to left (!) which means pc = V * M * pl states that the point in object coordinates pl is transformed by the model-matrix M (we are in world coordinates now) and then by the view-matrix V to get the point in camera coordinates pc (right-handed coordinate system).
    Thus said the view-matrix computed from the “eyePos” as the camera position, “target” as the position where the camera looks at and “up” as the normalized vector specifying which way is up (e.g. [0,1,0]) would be as follows:
    As said in the article:
    z-vector = normalize(target – eyePos)
    x-vector = normalize(z-vector x up)
    y-vector = normalize(x-vector x z-vector)
    The orientation-matrix Rv is thus:
    x-vector.x, y-vector.x, -z-vector.x, 0,
    x-vector.y, y-vector.y, -z-vector.y, 0,
    x-vector.z, y-vector.z, -z-vector.z, 0,
    0, 0, 0, 1
    Notice the negation of the z-vector.
    And the Translation Matrix Tv that moves the camera to the origin:
    1, 0, 0, -eyePos.x,
    0, 1, 0, -eyePos.y,
    0, 0, 1, -eyePos.z,
    0, 0, 0, 1,
    Now the view-matrix is V = Tv * Rv (as stated above this is to be read from right to left: first rotate, than translate).
    Thus after the ModelView Transformation the camera is the origin and looks along the negative z-axis.

    I hope that helps a little in terms of the OpenGL-concept of the view and the notation. I found it to be confusing too while looking at different sources, some of them mixing up concepts or notations or just not stating the fundamental assumptions.

    Best regards.
    Rob

    Reply ↓

  10. Please do find time to rewrite this post. I went to this article with confusion in my mind (I think this is the case for most of us who came here) but only get more confused after reading it. (In my case, it is due to 1) orientation matrix at line 8 (since it looks like a column-major matrix) and 2) the MVP calculating order). But thanks for the clarification in comment, I finally made my mind clear. But if comment can be updated into the post, it will be much better. Anyway, thanks for the post!

    Reply ↓

    • Joysword,

      I absolutely agree with you. I wrote this article very quickly (in about an hour I think) not knowing in advance how much attention it would receive (top hit in Google when searching for “view matrix”). In hindsight, I should have taken more time to explain the differences between left-handed and right-handed coordinate systems, column-major, and row-major matrices, and provided a few examples of how to implement a working camera model.

      Rewriting this article is definitely on my to-do list.

      Reply ↓

  11. Thank you. Very usefull. I’m using opengl plus opencv for augmented reality application. I’m retriving the position of the camera with cv::solvePnP and I had problem in visualizing correctly the camera as a 3° person view. The fact is simple as you clearly explained: cv::solvePnP get the position of the camera, and if I want to use this transformation as view matrix i have to invert it. thanks!

    Reply ↓

    • Albert, correct. The cv::solvePnP function gives you the camera’s extrinsic paramters (translation and rotation). In order to use these values as a view matrix you can use the following code:

      viewMatrix = inverse( R * translate(t) );

      or, a computationally friendly version:

      viewMatrix = transpose(R) * translate(-t);

      Where R is the 4×4 world-space rotation matrix that you got back from cv::solvePnP and converted to matrix from using cv::Rodrigues and t is the translation vector that you got from cv::solvePnP. The translate() function will build a 4×4 translation matrix from a 3-component vector.

      Here we can just take the transpose of R since we know it is orthonormalized.

      Reply ↓

  12. thank you! with this theory I’m trying to rewrite a gluUnproject function but I’m a little bit lost with the matrix calculi.. can you help me?

    Reply ↓

  14. Hi,
    thanks for the great explanation. However i’m a little bit confused with the first part. It says that a column major matrix M that first translates (T), then rotates (R) and then scales (S) a point must be constructed as follows: M = T*R*S. I think that the order is wrong. When M is constructed that way the point is scaled first, then rotated then translated.

    Reply ↓

    • Claus,

      This is a common misconception when dealing with column-major matrices. The order of transformations using column-major matrices must be read from left to right. Using row-major matrices the transformations are read right to left so the order of the transforms must be swapped:

      Column-major:
      [math]\mathbf{M}=\mathbf{T}*\mathbf{R}*\mathbf{S}[/math]

      Row-major:
      [math]\mathbf{M}=\mathbf{S}*\mathbf{R}*\mathbf{T}[/math]

      I have provided a demo at the end of the article that demonstrates this using column-major matrices. Try changing the order of transformations on line 434 of main.cpp to see what happens.

      Reply ↓

      • It says,
        M = T R S
        This transformation can be stated in words as “first translate, then rotate, then scale”.

        But I think it should be “first scale, then rotate, then translate.”

        Reply ↓

      • No, you are wrong, interestingly! I downloaded the code and checked 🙂 What line 434 does is first scale, then rotate around the center and lastly move the scaled and rotated box into its place. Right to left. Exactly like you do with the P*V matrix, first you move the camera into place (V) and then you apply projection (P).
        If you swap the rotation and the translation (M = R*T*S) then the rotation affects the translation and the boxes move around, i.e. each scaled box is translated and then rotated around the translation point. If you move the scaling to the left (M = S*T*R) then the whole field of boxes expands and contracts, i.e. the scaling affects the translation and rotation.

        Reply ↓

      • Don’t mean to be a dick here but how this is not a misconception. Column-major matrix multiplications must be read from right to left and that’s exactly why the code on line 434 of main.ccp actually works, because glm::matrix is column-major (https://glm.g-truc.net/0.9.2/api/a00001.html). The scaling is first applied, then the rotation, and then translation. Applying translation first and then doing rotations would get you some unwanted results. Source to back up what I’m saying, last paragraph of p.183 of Game Engine Architecture by Jason Gregory (lead programmer at Naughty Dog).

        Reply ↓

        • Martellino,

          This has always been a misconception for me too. It comes from the way I envision the transformation occuring. I envision that the basis space (the coordinate space) of the object is being transformed. If the basis space is first scaled then any transformation that occurs after that will occur in the scaled space (For example, if the object is scaled by 50% then it will only be translated half as much) but this is not true! The way I should have been thinking about it is that the transformations are always applied relative to the origin of the “global space” (For example, if the object is scaled 50% then the vertices will only be scaled local to the current global origin – if it was translated first then scaled, then the vertices would be scaled towards the global origin – probably turning the vertices into spaghetti, and if it was translated first then rotated, it would rotate around the global origin). I really should make a video that can demonstrate this confusion.

          Your reference to the Game Engine Architecture book by Jason Gregory helped me realize this with the following formula (for column vectors):

          \[\mathbf{v}’=(\mathbf{C}(\mathbf{B}(\mathbf{A}\mathbf{v})))\]

          Which is read from right-to-left: First transform \(\mathbf{v}\) by \(\mathbf{A}\), then transform the result by \(\mathbf{B}\), and finally transform the result by \(\mathbf{C}\).

          Although Jason clearly prefers row vectors as he uses row vectors for the rest of the text which may also be a source of confusion for some readers (including myself😕)

          Thanks for pointing this out Martellino. I’ve updated the article to reflect this.

          Reply ↓

      • I think this concepts are SUPER confusing and not explained fully in this article of the comments. I will try to do this, I’m not 100% sure my explanation will be correct. I think you confused the order of transformation in this comment too.

        In Column-Major mode Right-Hand matrix is transformed by the Left-Hand matrix, in Row-Major its other way around. So, in your Column-Major example:

        M = T * R * S;

        The first transformation is actually R that is Translated and then the scale is translated and rotated, so the actual order of transformations can be visualised like this:

        S -> (R -> T)

        In Row-Major mode its much more stritght forward process:

        (S -> R) -> T

        It is important to remember that operators in C/C++ does not care about matrix row/column modes. Operators work as defined by C/C++ standard – from left to right.

        Reply ↓

  15. Excellent article – thanks. Hope to see the arcball camera implementation documented. Also, is there a follow-up article planned which covers projection matrices?

    Reply ↓

    • Will,

      The arcball camera is slightly more complicated and requires a few functions to define correctly so I’m wondering how I’m going to approach that one.

      There is definitely an article about projection matrices planned but I probably won’t be able to get to it for another couple months…

      Reply ↓

  16. Do you have any lessons/explanations of the World transform matrix or model matrix? I am not sure on what these two matrices really are and how to construct them. By the way really good explanation, now it is a lot more clear !

    Reply ↓

  19. Hello friend, the link to download the “View Matrix Demo” does not work, please send me the code, I need to review it … thanks

    Reply ↓

  20. I find it odd that the demo code doesn’t even use the tutorial code here, instead it uses the glm library functions to translate orientation and position into the view matrix which is entirely different then what is shown here.

    Reply ↓

    • And in that case, wouldn’t it just be more simple to do:

      m_ViewMatrix = glm::translate(glm::toMat4(m_Rotation),-m_Position);

      Reply ↓

    • I wanted to keep the code in the tutorial as generic as possible, but at the same time I didn’t implement all of the math functions I needed to create the demo. Since the GLM math library provides the additional math functions, I used that in the demo source code. I just wanted to provide a “generic” solution in the text of the article.

      Reply ↓

  22. I’ve updated this article to include a section about an arcball (orbit) camera and corrected some misconceptions about the order of multiplications (column major matrix multiplication is read from right-to-left) thanks to Claus and martellino for pointing out these inconsistencies.

    Reply ↓

  24. Hi Jer,
    Thanks for this informative article! This article helped me a lot when implementing an arcball camera system. I found what you said is not quite accurate in regards to using euler angles won’t escape from the singularity problem at 90 degree angle. What is working for me is that I do transformations on the model matrix in the order of scaling, rotation (using pitch and yaw value of the object), translation and then inverse the matrix to finally multiply the resulting matrix to a classical lookAt function, as if the camera is stationary and looking at the object freely rotate, to obtain the view matrix. I don’t have a strong back ground in mathematics to explain what happen but I found out that this implementation stopped the problem of singularity from my earlier naive attempt.

    Reply ↓

    • Wanderking,

      When only applying a single (Euler) rotation will generally produce a correct result. And concatenating two rotation matrices (where each one represents a rotation in a separate axis) will also generally work. The problem with Euler angles occurs when you rotate one axis so that it aligns with another axis. (For example, applying a yaw of 90° will cause the \(\mathbf{Z}\) axis to become aligned with the global \(\mathbf{X}\) axis). The result is that rotations in either of the aligned axes will have the same effect!

      For example, assume that pitch (\(\alpha\)) represents a counterclockwise rotation about the \(\mathbf{X}\) axis and yaw (\(\beta\)) represents a counterclockwise rotation about the \(\mathbf{Y}\) axis. Then,

      \[ R_{pitch}(\alpha) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha \\ 0 & \sin\alpha & \cos\alpha \end{bmatrix} \]

      and,

      \[ R_{yaw}(\beta) = \begin{bmatrix} \cos\beta & 0 & \sin\beta \\ 0 & 1 & 0 \\ -\sin\beta & 0 & \cos\beta \end{bmatrix} \]

      And concatenating them gives,

      \[ R(\alpha,\beta) = \begin{bmatrix} \cos\beta & 0 & \sin\beta \\ \sin\alpha\sin\beta & \cos\alpha & -\sin\alpha\cos\beta \\ -\cos\alpha\sin\beta & \sin\alpha & \cos\alpha\cos\beta \end{bmatrix} \]

      And setting \(\beta=90°\) gives,

      \[ R(\alpha,90°) = \begin{bmatrix} 0 & 0 & 1 \\ \sin\alpha & \cos\alpha & 0 \\ -\cos\alpha & \sin\alpha & 0 \end{bmatrix} \]

      Now let’s add roll (\(\gamma\)) which is a counterclockwise rotation about the \(\mathbf{Z}\) axis:

      \[ R_{roll}(\gamma) = \begin{bmatrix} \cos\gamma & -\sin\gamma & 0 \\ \sin\gamma & \cos\gamma & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

      And concatenating this with the previous matrix gives:

      \[ \begin{array}{rcl} R(\alpha,90°,\gamma) & = & \begin{bmatrix} 0 & 0 & 1 \\ \sin\alpha\cos\gamma+\cos\alpha\sin\alpha & -\sin\alpha\sin\gamma+\cos\alpha\cos\gamma & 0 \\ -\cos\alpha\cos\gamma+\sin\alpha\sin\gamma & \cos\alpha\sin\gamma+\sin\alpha\cos\gamma & 0 \end{bmatrix} \\ & = & \begin{bmatrix} 0 & 0 & 1 \\ \sin(\alpha + \gamma) & \cos(\alpha+\gamma) & 0 \\ -\cos(\alpha+\gamma) & \sin(\alpha+\gamma) & 0 \end{bmatrix} \end{array} \]

      The result of either a change in pitch (\(\alpha\)) or a roll (\(\gamma\)) will only affect the pitch since the ability to roll has been lost due to the 90° yaw.

      For example, rotating the arbitrary point by \((90°, 90°, 0)\) has the same affect as rotating the point by \((0, 90°, 90°)\).

      A 90° pitch followed by a 90° yaw produces:

      \[ \begin{array}{rcl} R(90°,90°,0°) & = & \begin{bmatrix} 0 & 0 & 1 \\ \sin{90°} & \cos{90°} & 0 \\ -\cos{90°} & \sin{90°} & 0 \end{bmatrix} \\ \begin{bmatrix} z \\ x \\ y \end{bmatrix} & = & \begin{bmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} \end{array} \]

      And a 90° yaw followed by a 90° roll produces:

      \[ \begin{array}{rcl} R(0°,90°,90°) & = & \begin{bmatrix} 0 & 0 & 1 \\ \sin{90°} & \cos{90°} & 0 \\ -\cos{90°} & \sin{90°} & 0 \end{bmatrix} \\ \begin{bmatrix} z \\ x \\ y \end{bmatrix} & = & \begin{bmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} \end{array} \]

      Which is the exact same transformation! So by applying a 90° yaw results in a loss of one of the other two rotations. This is referred to as gimbal-lock although you may not experience it in your own implementation, it is still an issue that you must consider when implementing 3D rotations in your game!

      Reply ↓

  25. When you want to avoid gimble lock via direct matrix rotation id avoid yaw pitch roll, Instead rotate with a AxisAngle function x y z separately against the world or build the matrices for each rotation and then concencate them in order with the world. World = (((World * RotationMatrixX) * RotationMatrixY)* RotationMatrixZ); Note doing this will no longer give you a fixed camera with the up pointing in the system up direction, but it will also disallow gimble lock thru a series of x y z rotations.

    Reply ↓

    • Will,

      There are several issues with using matrices to represent rotations:

      1. If you perform a 90° rotation about the X axis (causing the Z axis to align with the Y axis) followed by an arbitrary rotation about the Z axis will result in a spin around the Y axis. This is the Gimbal lock problem that rotating 1 axis to align with another causes a loss of rotation about that axis (One less Degree of Freedom (DoF)).
      2. Matrix multiplication is not commutative. Changing the order of multiplication changes the result.
      3. It is difficult to perform an interpolation between rotation matrices (without decomposing the matrix first) without introducing skew in between (try to interpolate between the identity matrix and a rotation about any axis. What happens half-way through the interpolation?).

      See Understanding Quaternions for an alternative approach to using rotation matrices to represent rotations.

      Reply ↓

  26. Great article, i just would like to add one point:

    Column-major/Row-major do indeed affect the memory layout (see the Wikipedia page for “Row- and column-major order”). OpenGL simply means it treats vectors as column vectors, which is not really defining the memory layout.
    Maybe this is noteworthy.

    Reply ↓

    • John,

      Given structures:

      You can see that the memory layout doesn’t change. In row-major order, the memory is laid out “in rows” and in column-major order, memory is laid out “in columns”. So if you copy a row-major matrix into a column-major matrix or vice versa, you don’t need to transpose the matrix. You just have to swap the order of multiplications.

      Reply ↓

Leave a Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.