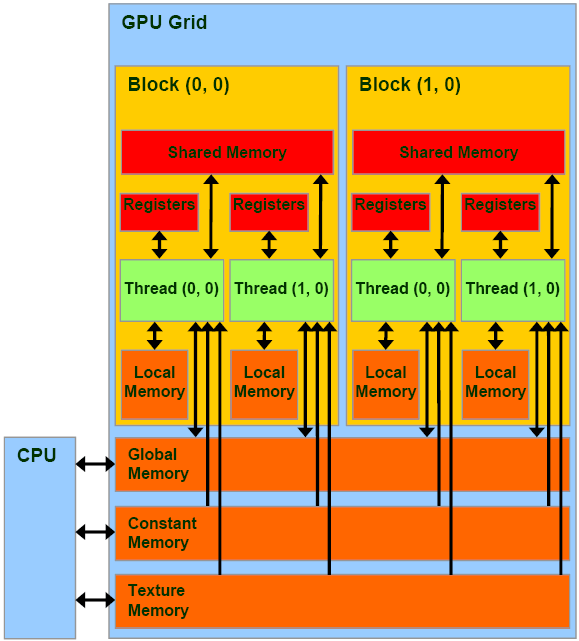
In this article, I will introduce the different types of memory your CUDA program has access to. I will talk about the pros and cons for using each type of memory and I will also introduce a method to maximize your performance by taking advantage of the different kinds of memory.
I will assume that the reader already knows how to setup a project in Microsoft Visual Studio that takes advantage of the CUDA programming API. If you don’t know how to setup a project in Visual Studio that uses CUDA, I recommend you follow my previous article titled [Introduction to CUDA]
Introduction
There are several different types of memory that your CUDA application has access to. For each different memory type there are tradeoffs that must be considered when designing the algorithm for your CUDA kernel.
Global memory has a very large address space, but the latency to access this memory type is very high. Shared memory has a very low access latency but the memory address is small compared to Global memory. In order to make proper decisions regarding where to place data and when, you must understand the differences between these memory types and how these decisions will affect the performance of your kernel.
In this article, I will describe the different memory types and show examples of using different memory to improve the performance of your kernel.
CUDA Memory Types
Every CUDA enabled GPU provides several different types of memory. These different types of memory each have different properties such as access latency, address space, scope, and lifetime.
The different types of memory are register, shared, local, global, and constant memory.
On devices with compute capability 1.x, there are 2 locations where memory can possibly reside; cache memory and device memory.
The cache memory is considered “on-chip” and accesses to the cache is very fast. Shared memory and cached constant memory are stored in cache memory with devices that support compute capability 1.x.
The device memory is considered “off-chip” and accesses to device memory is about ~100x slower than accessing cached memory. Global memory, local memory and (uncached) constant memory is stored in device memory.
On devices that support compute capability 2.x, there is an additional memory bank that is stored with each streaming multiprocessor. This is considered L1-cache and although the address space is relatively small, it’s access latency is very low.
In the following sections I will describe each type and when it is best to use that memory type.
Register
Scalar variables that are declared in the scope of a kernel function and are not decorated with any attribute are stored in register memory by default. Register memory access is very fast, but the number of registers that are available per block is limited.
Arrays that are declared in the kernel function are also stored in register memory but only if access to the array elements are performed using constant indexes (meaning the index that is being used to access an element in the array is not a variable and thus the index can be determined at compile-time). It is currently not possible to perform random access to register variables.
Register variables are private to the thread. Threads in the same block will get private versions of each register variable. Register variables only exists as long as the thread exists. Once the thread finishes execution, a register variable cannot be accessed again. Each invocation of the kernel function must initialize the variable each time it is invoked. This might seem obvious because the scope of the variable is within the kernel function, but this is not true for all variables declared in the kernel function as we will see with shared memory.
Variables declared in register memory can be both read and written inside the kernel. Reads and writes to register memory does not need to be synchronized.
Local
Any variable that can’t fit into the register space allowed for the kernel will spill-over into local memory. Local memory has the same access latency as global memory (that is to say, slow). Accesses to local memory are cached only only GPU’s with compute capability 2.x.
Like registers, local memory is private to the thread. Each thread must initialize the contents of a variable stored in local memory before it should be used. You cannot rely on another thread (even in the same block) to initialize local memory because it is private to the thread.
Variables in local memory have the lifetime of the thread. Once the thread is finished executing, the local variable is no longer accessible.
You cannot decorate a variable declaration with any attribute but the compiler will automatically put variable declarations in local memory under the following conditions:
- Arrays that are accessed with run-time indexes. That is, the compiler can’t determine the indices at compile time.
- Large structures or arrays that would consume too much register space.
- Any variable declared that exceeds the number of registers for that kernel (this is called register-spilling).
The only way you can determine if the compiler has put some function scope variables in local memory is by manual inspection of the PTX assembly code (obtained by compiling with the -ptx or -keep option). Local variables will be declared using the .local mnemonic and loaded using the ld.local mnemonic and stored with the st.local mnemonic.
Variables in local memory can be both read and written within the kernel and access to local memory does not need to be synchronized.
Variables that are decorated with the __shared__ attribute are stored in shared memory. Accessing shared memory is very fast (~100 times faster than global memory) although each streaming multiprocessor has a limited amount of shared memory address space.
Shared memory must be declared within the scope of the kernel function but has a lifetime of the block (as opposed to register, or local memory which has a lifetime of the thread). When a block is finished execution, the shared memory that was defined in the kernel cannot be accessed.
Shared memory can be both read from and written to within the kernel. Modification of shared memory must be synchronized unless you guarantee that each thread will only access memory that will not be read-from or written-to by other threads in the block. Block synchronization is acheived using the __syncthreads() barrier function inside the kernel function.
Since access to shared memory is faster than accessing global memory, it is more efficient to copy global memory to shared memory to be used within the kernel but only if the number of accesses to global memory can be reduced within the block (as we’ll see with the matrix multiply example that I will show later).
Global
Variables that are decorated with the __device__ attribute and are declared in global scope (outside of the scope of the kernel function) are stored in global memory. The access latency to global memory is very high (~100 times slower than shared memory) but there is much more global memory than shared memory (up to 6GB but the actual size is different across graphics cards even of the same compute capability).
Unlike register, local, and shared memory, global memory can be read from and written to using the C-function cudaMemcpy.
Global memory has a lifetime of the application and is accessible to all threads of all kernels. One must take care when reading from and writing to global memory because thread execution cannot be synchronized across different blocks. The only way to ensure access to global memory is synchronized is by invoking separate kernel invocations (splitting the problem into different kernels and synchronizing on the host between kernel invocations).
Global memory is declared on the host process using cudaMalloc and freed in the host process using cudaFree. Pointers to global memory can be passed to a kernel function as parameters to the kernel (as we will see in the example later).
Reads from global memory is cached only on devices that support compute capability 2.0 but any write to global memory will invalidate the cache thus eliminating the benefit of cache. Access to global memory on devices that support compute capability 1.x is not cached.
It is a bit of an art-form to reduce the number of accesses to global memory from within a kernel by using blocks of shared memory because the access latency to shared memory is about 100 times faster than accessing global memory. Later, I will show an example of how we can reduce the global memory access using shared memory.
Constant
Variables that are decorated with the __constant__ attribute are declared in constant memory. Like global variables, constant variables must be declared in global scope (outside the scope of any kernel function). Constant variables share the same memory banks as global memory (device memory) but unlike global memory, there is only a limited amount of constant memory that can be declared (64KB on all compute capabilities).
Access latency to constant memory is considerably faster than global memory because constant memory is cached but unlike global memory, constant memory cannot be written to from within the kernel. This allows constant memory caching to work because we are guaranteed that the values in constant memory will not be changed and therefor will not become invalidated during the execution of a kernel.
Constant memory can be written to by the host process using the cudaMemcpyToSymbol function and read-from using the cudaMemcpyFromSymbol function. As far as I can tell, it is not possible to dynamically allocate storage for constant memory (the size of constant memory buffers must be statically declared).
Like global memory, constant memory has a lifetime of the application. It can be accessed by all threads of all kernels and the value will not change across kernel invocations unless explicitly modified by the host process.
Properties of Memory
The amount of memory that is available to the CUDA application is (in most cases) specific to the compute capability of the device. For each compute capability, the size restrictions of each type of memory (except global memory) is defined in the table below. The application programmer is encouraged to query the device properties in the application using the
cudaGetDeviceProperties method.
| Technical Specifications | 1.0 | 1.1 | 1.2 | 1.3 | 2.0 |
| Number of 32-bit registers per MP | 8 K | 16 K | 32 K | ||
| Maximum amount of shared memory per MP | 16 KB | 48 KB | |||
| Amount of local memory per thread | 16 KB | 512 KB | |||
| Constant memory size | 64 KB | ||||
The following table summarizes the different memory types and the properties of those types.
| Memory | Located | Cached | Access | Scope | Lifetime |
| Register | cache | n/a | Host: None Kernel: R/W |
thread | thread |
| Local | device | 1.x: No 2.x: Yes |
Host: None Kernel: R/W |
thread | thread |
| Shared | cache | n/a | Host: None Kernel: R/W |
block | block |
| Global | device | 1.x: No 2.x: Yes |
Host: R/W Kernel: R/W |
application | application |
| Constant | device | Yes | Host: R/W Kernel: R |
application | application |
Pointers to Memory
You can use pointers to memory in a kernel but you must be aware that the pointer type does not determine where the memory is located.
For example, the following code declares a pointer to constant memory and a pointer to global memory. You should be aware that only the pointer variable is constant – not what it points to.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
__constant__ float* constPtr; __device__ float* globalPtr; __global__ void KernelFunction(void) { // Assign the pointer to global memory to a pointer to constant memory. // This will not compile because the pointer is constant and you can't change // what a const-pointer points to in the kernel. constPtr = globalPtr; // This will compile because what the const pointer points to is not // necessarily const (if it is, you'll probaly get a runtime error). *constPtr = *globalPtr; } |
Since you can’t dynamically allocate constant memory, this example would not be very useful anyways.
Be careful when using pointers like this. It is a best-practice rule to ensure that a declared pointer only points to one type of memory (so a single pointer declaration will only point to global memory and another pointer declaration will only point to shared memory).
Minimize Global Memory Access
Since access latency is much higher for global memory than it is for shared memory, it should be our objective to minimize accesses to global memory in favor of shared memory. This doesn’t mean that every access to data in global memory should first be copied into a variable in shared (or register) memory. Obviously we will not benefit from the low latency shared memory access if our algorithm only needs to make a single access to global memory. But it happens in some cases that multiple threads in the same block will all read from the same location in global memory. If this is the case, then we can speed-up our algorithm by first allowing each thread in a block to copy one part of the global memory into a shared memory buffer and then allowing all of the threads in a block to access all elements in that shared memory buffer.
To demonstrate this, I will show several flavors the classic matrix multiply example. The first example I will show is the standard implementation of the matrix multiply using only global memory access. Then, I will show an optimized version of the algorithm that uses shared memory to reduce the number of accesses to global memory for threads of the same block.
Matrix Multiply using Global Memory
This version of the matrix multiply algorithm is the easiest to understand however it is also a very naive approach.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
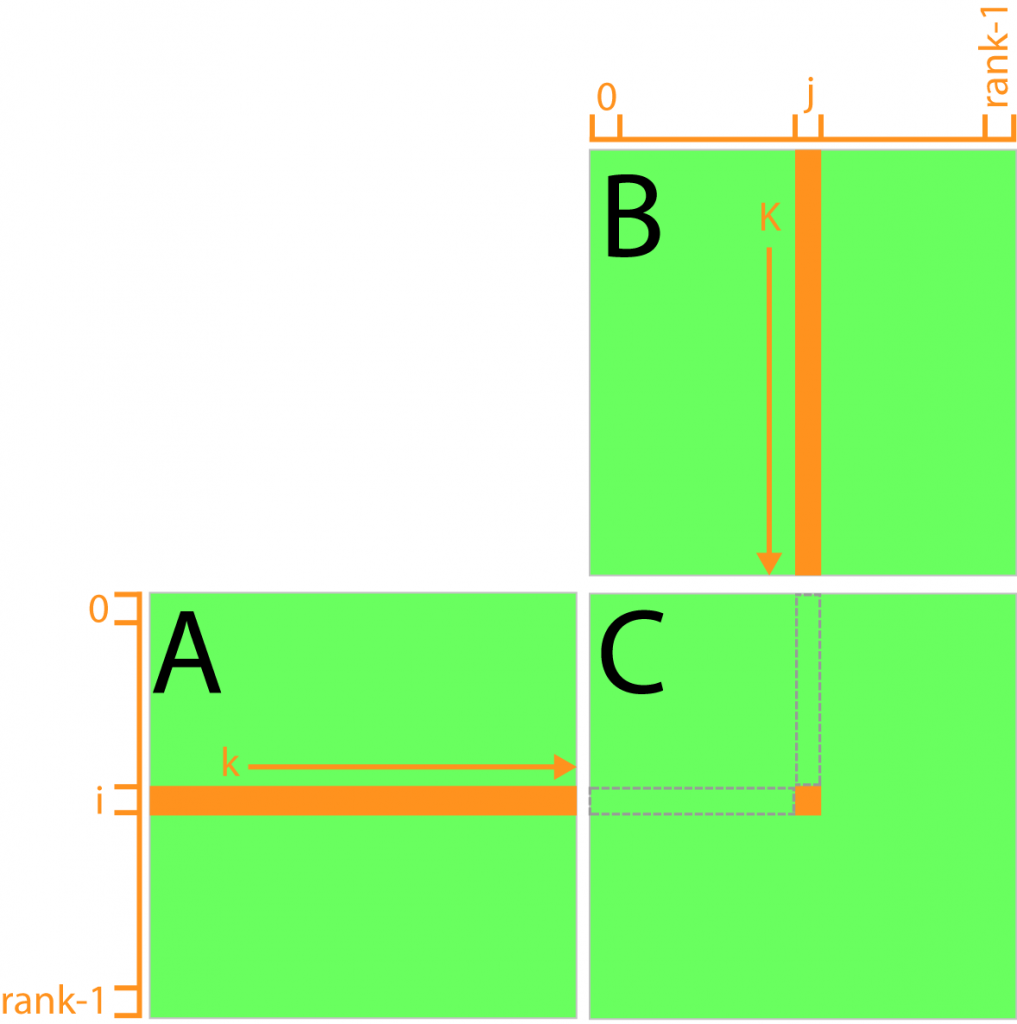
__global__ void MatrixMultiplyKernel_GlobalMem( float* C, const float* A, const float* B, unsigned int rank ) { // Compute the row index unsigned int i = ( blockDim.y * blockIdx.y ) + threadIdx.y; // Compute the column index unsigned int j = ( blockDim.x * blockIdx.x ) + threadIdx.x; unsigned int index = ( i * rank ) + j; float sum = 0.0f; for ( unsigned int k = 0; k < rank; ++k ) { sum += A[i * rank + k] * B[k * rank + j]; } C[index] = sum; } |
The parameters A, B, and C all point to buffers of global memory.
The fist step is to figure out which row (i) and which column (j) we are operating on for this kernel.
On line 10, we loop through all of the elements of row i of matrix A and the column j of matrix B and compute the summed product of corresponding entries (the dot product of row i and column j). A visual aid of this algorithm is shown below.
If we analyze this algorithm, we may notice that the same row elements of matrix A are being accessed for every resulting row element of matrix C and all the column elements of matrix B are being accessed for every resulting column element of matrix C. If we say that the resulting matrix C is N x M elements, then each element of matrix A is being accessed M times and each element of matrix B is being accessed N times. That seems pretty wasteful to me.
What if we could reduce the number of times the elements of matrix A and B are accessed to just 1? Well, depending on the size of our matrix, we could just store the contents of matrix A and matrix B into shared memory buffers then just compute the resulting matrix C from those buffers instead. This might work with small matrices (remember that shared memory is local to a single block and with compute capability 1.3, we are limited to matrices of about 20 x 20 because we are limited to 512 threads that can be assigned to a single block).
But what if we had larger matrices to multiply? If we can find a way to split the problem into “phases” then we could simply load each “phase” into shared memory, process that “phase”, then load the next “phase” and process that one until we have exhausted the entire domain.
This technique of splitting our problem domain into phases is called “tiling” named because of the way we can visualize the technique as equal sized tiles that represent our problem domain.
For this particular problem, the best partitioning of the problem domain is actually the same as partitioning of the grid of threads that are used to compute the result.
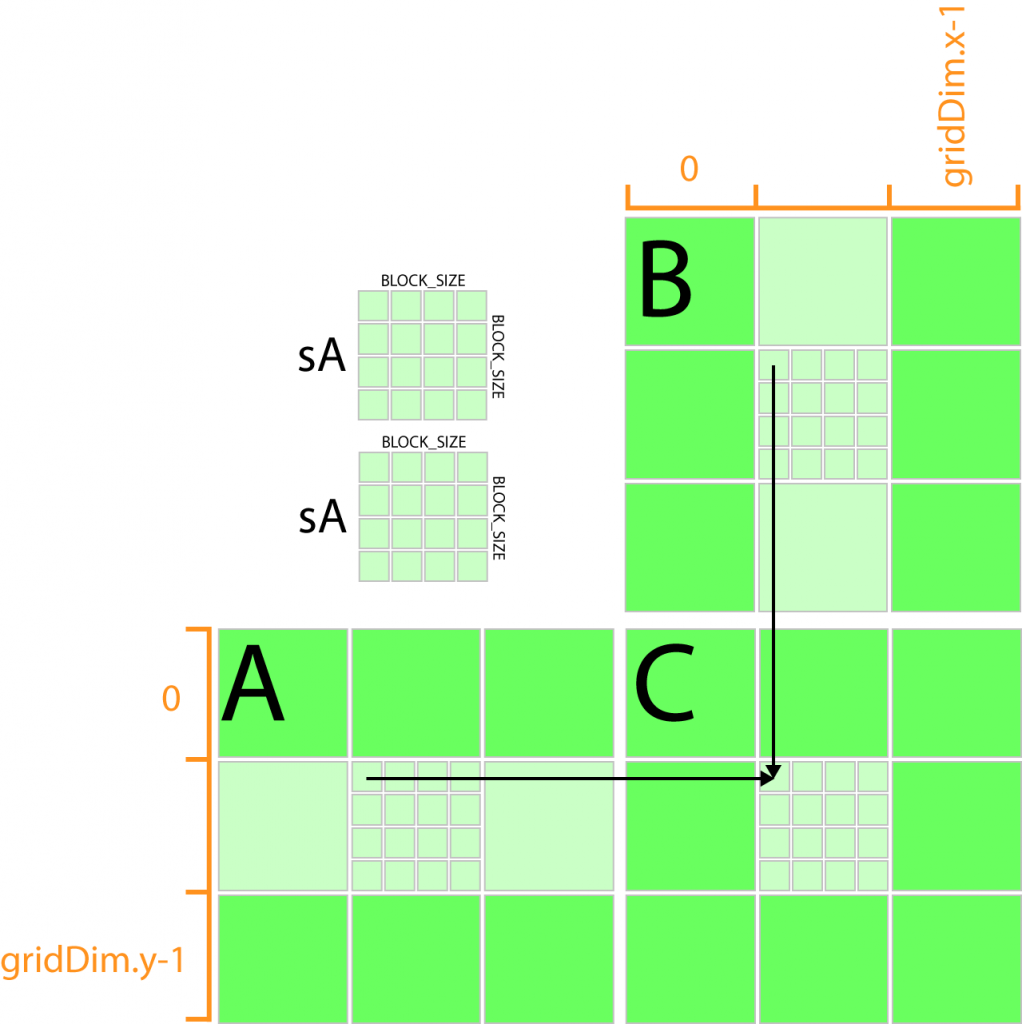
If we split our grid into blocks of 16 x 16 threads (which I showed in a previous article about the CUDA execution model to be a good granularity for this problem) then we can create two buffers in shared memory that are the same size as a single block in our kernel grid, one that holds a “tile” of matrix A, and other to store a “tile” of matrix B.
Let’s see how this might look:
So the idea is simple, each thread block defines a pair of shared memory buffers that are used to “cache” a “tile” of data from matrix A and matrix B. Since the “tile” is the same size as the thread block, we can just let each thread in the thread block load a single element from matrix A into one of the shared memory buffers and a single element from matrix B into the other. Using this technique, we can reduce the number of global memory access to rank / BLOCK_SIZE per thread (where BLOCK_SIZE is the size of the thread block and shared memory buffer in a single dimension).
But will this work? We only have access to 16 KB (16,384 Bytes) of shared memory per streaming multiprocessor for devices of compute capability 1.x. If our BLOCK_SIZE is 16 then we need 162 floating point values (4-bytes each) per shared memory buffer. So the size in bytes of each shared memory buffer is:
[math]\begin{matrix}bufferSize & = & 16^{2}\cdot4 \\ bufferSize & = & 256\cdot4 \\ bufferSize & = & 1024\end{matrix}[/math]And we need 2 buffers, so we will need 2,048 Bytes of shared memory per block. If you remember from the previous article about the CUDA thread execution model,
thread blocks of size 16 x 16 will allow 4 resident blocks to be scheduled per streaming multiprocessor. So 4 blocks each requiring 2,048 Bytes gives a total requirement of 8,192 KB of shared memory which is 50% of the available shared memory per streaming multiprocessor. So this this tiling strategy will work.
So let’s see how we might implement this in the kernel.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
#define BLOCK_SIZE 16 __global__ void MatrixMultiplyKernel_SharedMem( float* C, const float* A, const float* B, unsigned int rank ) { unsigned int tx = threadIdx.x; unsigned int ty = threadIdx.y; unsigned int bx = blockIdx.x; unsigned int by = blockIdx.y; // Allocate share memory to store the matrix data in tiles __shared__ float sA[BLOCK_SIZE][BLOCK_SIZE]; __shared__ float sB[BLOCK_SIZE][BLOCK_SIZE]; // Compute the column index unsigned int j = ( blockDim.x * bx ) + tx; // Compute the row index unsigned int i = ( blockDim.y * by ) + ty; unsigned int index = ( i * rank ) + j; float sum = 0.0f; // Loop through the tiles of the input matrices // in separate phases of size BLOCK_SIZE for( unsigned int phase = 0; phase < rank/BLOCK_SIZE; ++phase ) { // Allow each thread in the block to populate the shared memory sA[ty][tx] = A[i * rank + (phase * BLOCK_SIZE + tx)]; sB[ty][tx] = B[(phase * BLOCK_SIZE + ty) * rank + j]; __syncthreads(); for( unsigned int k = 0; k < BLOCK_SIZE; ++k ) { sum += sA[ty][k] * sB[k][tx]; } __syncthreads(); } C[index] = sum; } |
On line 5-8, we just store some “shorthand” versions of the thread and block indexes into private thread variables (these are stored in registers).
On line 11, and 12 the two shared memory buffers are declared to store enough values that each thread in the thread block can store a single entry in the arrays.
On line 15, the index of the column is computed and stored in another registry variable j and on line 16, the row is computed and stored in registry variable i.
On line 20, the 1-D index into the result matrix C is computed and the sum of the products is stored in the float variable sum.
On line 25, we will loop over the “tiles” (called phases here) of matrix A and matrix B. You should note that this algorithm assumes the size of the matrix is evenly divisible by the size of the thread block.
On lines 28 and 29 is where the magic happens. Since the shared memory is accessible to every thread in the block, we can let every thread in the block copy 1 element from matrix A and one element from matrix B into the shared memory blocks.
Before we can access the data in the shared memory blocks, we must ensure that all threads in the entire block have had a chance to write their data. To do that we need to synchronize the execution of all the threads in the block by calling the __syncthreads() method.
Then the for loop on line 32 will loop through the elements of shared memory and sum the products.
Before we leave this loop and start filling the next “tile” into shared memory, we must ensure that all threads are finished with the shared memory buffers. To do that, we must execute __syncthreads() again on line 36.
This will repeat until all phases (or tiles) of the matrix have been processed.
Once all phases are complete, then the value stored in sum will contain the final result and it is written to the destination matrix C.
Running the global memory version of the matrix multiply on my laptop with a 512 x 512 matrix runs in about 45 milliseconds. Running the shared memory version on the same matrix completes in about 15 milliseconds (including copying memory from host to device and copying the result back to host memory). This provides a speed-up of 300%!
Resources as a Limiting Constraint
It is entirely possible to allocate more shared memory per block than 2,048 bytes, but the block scheduler will reduce the number of blocks scheduled on a streaming multiprocessor until the shared memory requirements are met. If you want to allocate all 16 KB of shared memory in a single block, then only a single block will be resident in the streaming multiprocessor at any given moment which reduce the occupancy of the streaming multiprocessor to 25% (for a 16 x 16 thread block on compute capability 1.3).
This of course is not ideal, but it is conceivable to imagine that a single block might have this requirement. In most cases the GPU will still out-perform the CPU if the benefit of using the low-latency memory is fully realized.
This is also true for the number of registers that can be allocated per block. If a single kernel declares 32 32-bit variables that must be stored in registers and the thread block consists of 16 x 16 threads, then the maximum number of blocks that can be active in a streaming multiprocessor on a device with compute capability 1.3 is 2 because the maximum number of 32-bit registers that can be used at any moment in time is 16,384.
[math]\begin{matrix}numRegisters & = & 16^{2}\cdot32 \\ numRegisters & = & 256\cdot32 \\ numRegisters & = & 8192\end{matrix}[/math]So the number of 32-bit registers/block is 8,192. So the streaming multiprocessor can accommodate a maximum of 16,384 / 8,192 = 2 blocks.
Exercise
Q. If we want to execute a 32 x 32 kernel grid consisting of 16 x 16 thread blocks on a GPU, then what is the maximum amount of shared memory that we can allocate in a kernel function and still achieve 100% thread occupancy on the streaming multiprocessor for devices that support compute capability:
- 1.3?
- 2.0?
A. To properly answer this question, we must first know something about the limitations of the streaming multiprocessor.
Let’s first consider devices with compute capability 1.3:
We know from the previous article on the CUDA execution model, a warp consist of 32 threads. For devices of compute capability 1.3, the maximum number of resident warps is 32. This means that the SM can have a maximum of 1024 threads resident at any given time. With thread blocks consisting of 256 threads, we can have 1024/256 = 4 thread blocks resident per SM. We also know (from the compute capability table shown above) that for devices with compute capability 1.3, each SM has 16 KB (16,384 Bytes) of shared memory. In order to accommodate all 4 blocks, we cannot allocate more than 16 / 4 = 4 KB (4,096 Bytes) of shared memory per block if we want to achieve 100% occupancy.
For devices of compute capability 2.0:
Devices that support compute capability 2.0 can have a maximum of 48 active warps per SM with each warp consisting of 32 threads. This means the SM can accommodate a maximum of 32 * 48 = 1,536 threads per SM. So the maximum number of thread blocks that we can have on the SM is 1,536 / 256 = 6 thread blocks. According to the compute capability table shown above, devices that support compute capability 2.0 can have a maximum of 48 KB (49,152 Bytes) of shared memory per SM. In order to maintain 100% thread occupancy, we must not exceed 48 / 6 = 8 KB (8,192 Bytes) of shared memory per block.
Q. Given the same case as the previous question, what is the maximum number of 32-bit registers that can declared per thread while still maintaining 100% thread occupancy?
Conclusion
In this article, I discussed the different types of memory that is available on the CUDA GPU and I discussed the limitations and benefits of each type of memory. I also showed an example of using shared memory to optimize the performance of the matrix multiply kernel.
When creating a kernel function, the developer should always be aware of the resource limitations of the GPU and the effect that it will have on the ability for the block scheduler to fully occupy the streaming multiprocessor.
Demo
You can download the CUDA example below. This file contains a solution file for Visual Studio 2008 (v9). You must have the CUDA Toolkit installed to build from source. Pre-built executables are also provided in the bin folder for each project.
References
 Kirk, David B. and Hwu, Wen-mei W. (2010). Programming Massively Parallel Processors. 1st. ed. Burlington, MA 01803, USA: Morgan Kaufmann Publishers. |
| NVIDIA Corporation (2011, May). NVIDIA CUDA C Programming Guide. (Version 4.0). Santa Clara, CA 95050, USA Available from: http://developer.download.nvidia.com/compute/cuda/4_0/toolkit/docs/CUDA_C_Programming_Guide.pdf. Accessed: 15 November 2011. |
| NVIDIA Corporation (2009, January). NVIDIA’s Next Generation CUDA Compute Architecture: Fermi. (V1.1). Santa Clara, CA 95050, USA Available from: http://www.nvidia.com/content/PDF/fermi_white_papers/NVIDIA_Fermi_Compute_Architecture_Whitepaper.pdf. Accessed: 15 November 2011. |